용어 정의
- 시행(Experiment) : 무작위로 결정되는 현상을 관찰하는 과정
- 표본 공간(Sample Space) : 시행에서 발생 가능한 모든 경우의 집합
- 사건(Event) : 표본 공간의 모든 부분집합
확률의 단순한 정의(Naive definition of Probability)
1. 모든 사건이 발생할 확률이 같다.
2. 표본 공간이 유한하다.
위 두 가지를 만족한다고 가정할 때, 확률은 아래와 같은 식으로 정의할 수 있다.
P(A)=사건A가발생하는경우의수발생가능한모든경우의수
셈의 법칙(Principle of Counting)
- 곱의 법칙 : 각각의 시행에서 발생 가능한 경우의 수가 n1,n2,...,nr일 때, 발생 가능한 모든 경우의 수는 n1×n2×...×nr이다.
곱의 법칙을 이용해 포커에서 풀하우스가 나올 확률을 계산해보면 다음과 같다.
P(fullhouse)=13⋅(43)⋅12⋅(42)(525)
분모는 가능한 모든 경우의 수는 52개의 카드 중 5장을 뽑는 것이고, 분자는 13개의 종류 중 1가지를 택하는 경우의 수, 4가지 문양 중 3가지를 택하는 경우의 수, 나머지 12가지 종류 중 1가지를 택하는 경우의 수, 4가지 문양 중 2가지를 택하는 경우의 수를 모두 곱하여 구할 수 있다.
이항계수(Binomial Coefficient)
크기 n의 집합에서 순서 상관 없이 만들 수 있는 크기 k인 부분집합의 수
(nk)=n!(n−k)!k!
(nk)=0if(k>n)
표본 추출 표(Sampling Table)
n개 중에서 k개 뽑는 경우의 수를 복원 여부, 순서 여부에 따라 아래와 같이 나타낼 수 있다.
| 순서 O | 순서 X | |
| 복원 | nk | (n+k−1k) |
| 비복원 | n×(n−1)×...×(n−k+1) =n!(n−k)! |
(nk) |
- 복원, 순서 O인 경우
n개 중 1개를 고르는 것을 k번 반복한다. 곱의 법칙에 따라 nk인 것을 알 수 있다.
- 비복원, 순서 O인 경우
n개 중 1개 고르기, n-1개 중 1개 고르기, ... , n-k+1개 중 1개 고르기. 마찬가지로 곱의 법칙에 따라 $= \frac{n!}{(n-k)!}$인 것을 알 수 있다.
- 비복원, 순서 X인 경우
이 경우는 이항계수 자체이기 때문에 (nk)이다.
- 복원, 순서 X인 경우
이 때 경우의 수는 (n+k−1k)로 알려져 있다.
이 경우에는 조금 더 엄밀한 증명이 필요하다.
먼저, 숫자를 대입해서 확인해보자.
k = 1인 경우, (n1)=n
k = 0인 경우, (n−10)=1
n = 2인 경우, (k+1k)=(k+11)=k+1
n = 2인 경우를 조금 더 자세히 살펴보면, 상자 2개에 k개의 똑같은 물건을 집어넣는다고 생각할 수 있다.
이 때, 상자 1과 상자 2로 구분해서 생각해보면, 상자 1에 들어갈 수 있는 물건의 갯수는 0개에서 k개로 k+1가지 경우가 있고, 상자 1에 들어가는 물건의 갯수가 정해지면 상자2도 자동으로 정해지기 때문에 총 가능한 경우의 수는 k+1로 (n+k−1k)이 맞다는 것을 확인할 수 있다.
위 사례를 통해 일반화를 시켜보면, n개중 k개를 복원하면서, 순서에 상관 없이 뽑는 것은 곧 n개의 서로 다른 상자에 k개의 똑같은 물건을 넣는 것과 같다고 생각할 수 있다.
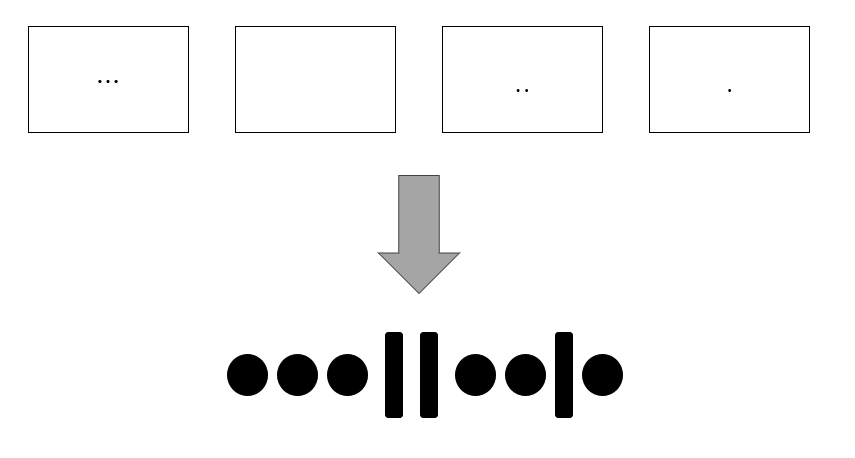
예를 들어서, n = 4, k = 6 이라면 상자 4개에 똑같은 물건 6개를 집어넣는 것이고, 물건을 점, 상자 사이를 구분선으로 구분하면 그림과 같이 표현할 수 있다.

위 그림과 같이 점 6개(k)와 막대기 3개(n-1)를 나열하는 경우의 수와 같고, 이는 k+(n-1)개의 자리 중 k개 혹은 n-1개의 자리를 고르는 것이므로 경우의 수는 (n+k−1k)가 된다.
해석을 통한 증명(Story Proof)
표본 추출 표에서 복원, 순서 X인 경우에 나올 수 있는 경우의 수를 증명할 때처럼 해석을 통해 증명하는 것도 중요하다.
또한, 해석을 통해 증명할 때 대수적으로 증명할 때 보다 더 쉽게 이해할 수 있는 경우도 있다.
- (nk)=(nn−k)
n명 중 k명을 뽑으면 남은 n-k명은 자동으로 정해지므로, 위의 식은 당연하게 받아들일 수 있다.
- n(n−1k−1)=k(nk)
이 경우는 n명의 사람 중 1명의 대표를 갖는 k명의 사람을 뽑는 경우로 이해하면 된다. 이건 두 가지 방법으로 가능하다.
동아리에 들어갈 사람 k명을 먼저 뽑고, k명 중 대표 1명을 뽑는 경우((nk)×k)
n명 중 대표를 1명 뽑고, 나머지 n-1명 동아리에 들어갈 사람 k-1명을 뽑는 경우(n×(nk))
따라서 n(n−1k−1)=k(nk)가 맞다는 것을 증명할 수 있다.
- (m+nk)=∑j=0k(mj)(nk−j) (Vandermond equation)
m+n명 중 k명을 뽑는 모든 경우는 아래 표와 같이 나눌 수 있다.
| m명 그룹 | n명 그룹 |
| 0 | k |
| 1 | k-1 |
| 2 | k-2 |
| ... | ... |
| k | 0 |
m명 그룹에서 몇명을 뽑을지 결정하면 n명 그룹에서는 자동으로 결정되기 때문에 (m+nk)=∑j=0k(mj)(nk−j) 이 맞다는 것을 바로 알 수 있다.
비둘기집 원리(Pigeonhole Principle)
n마리의 비둘기와 m개의 비둘기집이 있을 때, 만약 n>m이면 적어도 하나의 집에는 두 마리의 비둘기가 있다는 원리이다.
만약 비둘기가 11마리, 비둘기집이 10개 있을 때:
1. 모든 비둘기는 비둘기집이 있다.
2. 모든 비둘기집에는 1마리의 비둘기만 산다.(이 가정을 검토해보자)
만약 "모든 비둘기집에 1마리의 비둘기만 산다." 라는 가정이 참이라면, 총 비둘기의 수는 최대 10마리밖에 될 수 없다. 하지만 실제로 비둘기는 11마리이므로, 이 가정은 성립할 수 없다. 즉, 어떤 비둘기 집에는 두 마리 이상의 비둘기가 들어가야 한다.
확률의 엄밀한 정의(Non-Naive definition of Probability)
수학적으로 조금 더 엄밀한 방식으로 확률을 정의하는 접근으로, 공리적 확률(Axiomatic Probability)또는 콜모고로프 확률이라고 한다.
공리적 확률에서는 확률을 다음과 같은 세 가지 공리(axioms)로 정의한다.
1. 확률은 0 이상이어야 한다.
P(A)≥0
2. 전체 표본공간의 확률은 1이고, 공집합의 확률은 0이다.
P(ϕ)=0,P(S)=1
3. 서로소인 사건들의 합집합은 각 사건들의 확률의 합이다.
P(n=1⋃∞An)=n=1∑∞P(An)
확률의 주요 성질(Properties of Probability)
1. P(AC)=1−P(A)
증명
1=P(S)=P(A∪AC)...공리.2
1=P(A)+P(AC)...공리.3
A와AC는 서로소이므로 더할 수 있다.
2. IfA⊆B,thenP(A)≤P(B)
증명
B=A∪(B∩AC)
P(B)=P(A)+P(B∩AC)>=P(A)...공리.1,공리.2
B를 A가 포함된 부분, A가 포함되지 않은 부분으로 나눈다.(서로소로 만든다)
확률은 0보다 크거나 같기 때문에 P(A)+P(B∩AC)는 P(A)보다 크거나 같다.
3. P(A∪B)=P(A)+P(B)−P(A∩B)
증명
P(A∪B)=P(A∪(B∩AC))
=P(A)+P(B∩AC)...공리.3
P(A)+P(B∩AC)=P(A)+P(B)−P(A∩B)
P(B∩AC)+P(B∩A)=P(B)가 참이라면 위 식을 만족한다.
B∩AC,B∩A는 B를 서로소인 두 부분으로 나누것이므로 둘의 합집합은 B가 된다.
따라서 P((B∩AC)∪(B∩A)=P(B)이므로 위 식이 참임을 증명할 수 있다.
포함-배제 원리(General inclusion exclusion formula)
포함-배제 원리는 두 개 이상의 합사건의 확률 계산에 유용하게 사용되며, 확률의 주요 성질 3번을 확장하여 일반화 할 수 있다.
n개의 사건 A1,A2,...,An이 있다면, 아래와 같이 일반화 할 수 있다.
P(A1∪A2∪⋯∪An)=n∑i=1P(Ai)−∑1≤i<j≤nP(Ai∩Aj)+∑1≤i<j<k≤nP(Ai∩Aj∩Ak)−⋯+(−1)n+1P(A1∩A2∩⋯∩An)
또는
P(n⋃i=1Ai)=n∑k=1(−1)k+1∑1≤i1<i2<⋯<ik≤nP(Ai1∩Ai2∩⋯∩Aik)
1. 각 사건의 확률을 모두 더한다.
2. 두 개씩 겹치는 부분을 빼준다.
3. 세 개씩 겹치는 부분을 더해준다.
...
위 과정을 반복함으로써 계산할 수 있다.
매칭 문제(deMontmort's Problem)
1부터 n까지의 번호가 매겨진 카드를 무작위로 섞었을 대, 카드가 놓여진 순서(첫번째, 두번째)와 카드에 매겨진 숫자가 일치할 확률을 구하는 문제이다.
고유 순열로 해결할 수 있지만, 위에서 배운 포함-배제의 원리를 통해서도 이 문제를 해결할 수 있다.
먼저, Aj를 j번째 카드를 뒤집었을 때 그 카드에 j가 적혀져 있는 사건이라고 하자.
P(Aj)=1n
P(A1∩A2)=(n−2)!n!=1n(n−1)
P(A1∩A2∩...∩Ak)=(n−k)!n!
포함 배제 원리를 사용하여 합집합의 확률을 전개하면 아래와 같다.
P(A1∪A2∪⋯∪An)=n⋅1n−(n2)⋅1n(n−1)+(n3)⋅1n(n−1)(n−2)−⋯+(−1)n+1(nn)⋅1n!
P(A1∪A2∪⋯∪An)=n∑k=1(−1)k+1(nk)1n(n−1)…(n−k+1)
P(A1∪A2∪⋯∪An)=n∑k=1(−1)k+11k!
=1−1e...(TaylorSeries)